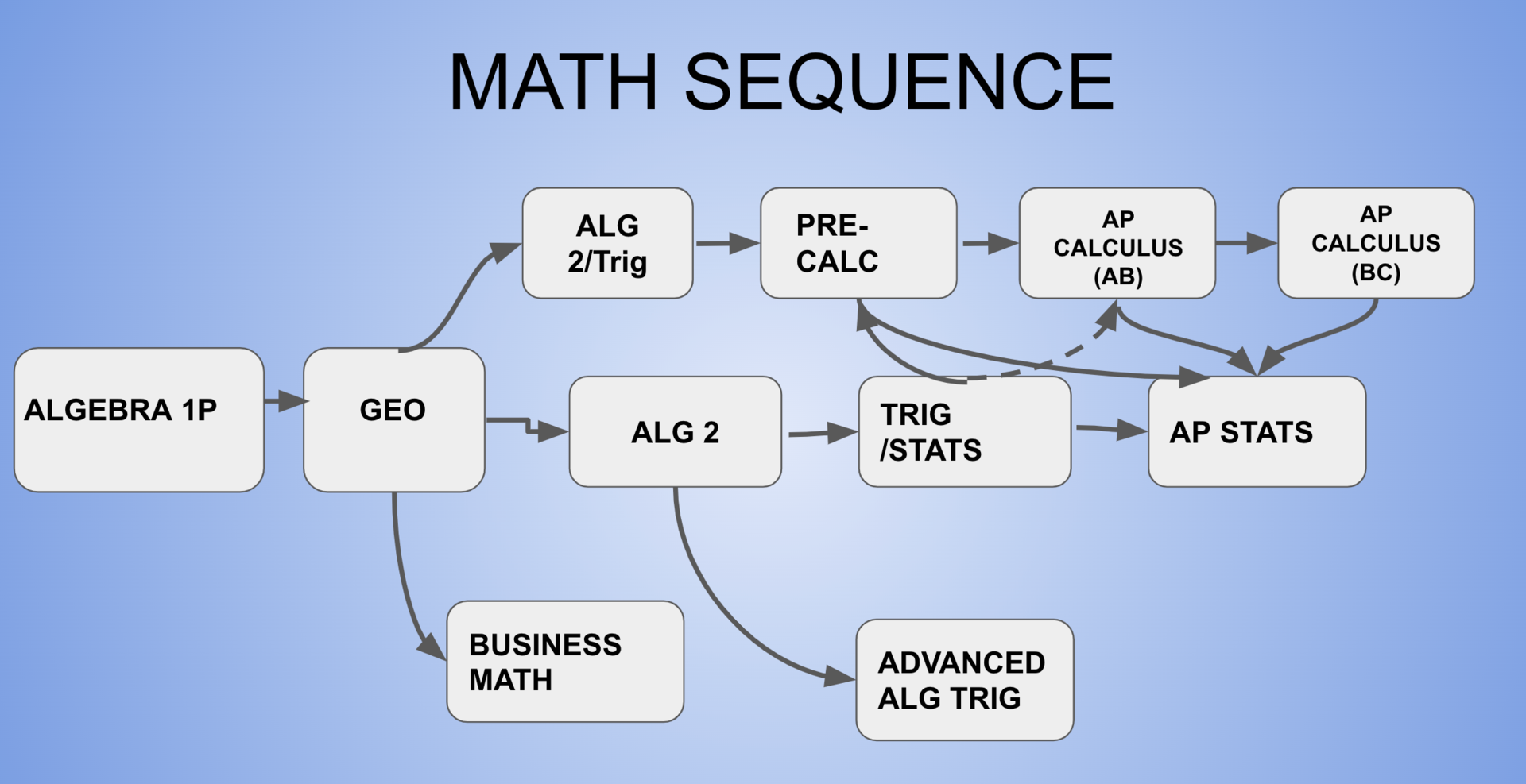
Mathematics is a subject that both challenges and rewards students as they progress through their academic journey. High school is a crucial time for developing mathematical skills, and many students will encounter math classes that push their limits, requiring both perseverance and a strong foundation in earlier coursework. Whether you're aiming to pursue a career in STEM or simply looking to strengthen your problem-solving abilities, understanding the hardest math classes in high school can help you better prepare and succeed.
In this article, we will dive into some of the most difficult math courses high school students may face, exploring what makes them challenging, what to expect, and how to navigate them successfully.
1. Advanced Placement (AP) Calculus
Overview
AP Calculus is often regarded as one of the toughest math classes in high school due to the complexity of the concepts and the depth of mathematical understanding required. The course comes in two forms: AP Calculus AB, which is roughly equivalent to a first-semester college calculus course, and AP Calculus BC, which covers both first and second-semester college calculus material.
What You’ll Learn
In AP Calculus, students delve into the study of limits, derivatives, integrals, and infinite series. These concepts are foundational to many advanced areas of mathematics, and students are expected to apply them to solve a variety of complex problems. Topics such as the chain rule, implicit differentiation, and integration by parts often prove to be challenging for students who are not confident in their algebraic and trigonometric skills.
Challenges and Expectations
- Problem-Solving: Expect rigorous problem-solving exercises that test your ability to apply theoretical knowledge to practical scenarios. Questions can range from straightforward calculations to multi-step problems that require deep analytical thinking.
- Homework: Assignments are typically extensive and time-consuming, often requiring students to complete multiple practice problems to fully grasp each concept.
- Exams: The AP Calculus exam is notoriously difficult, demanding strong analytical skills and time management, as students must answer complex questions within a limited timeframe.
How to Succeed
To excel in AP Calculus, students must have a solid foundation in algebra and trigonometry. Consistent practice, attending study groups, and seeking help from teachers when needed are crucial. Online resources like Khan Academy and Paul’s Online Math Notes can provide extra support.
2. Advanced Topics in Mathematics
Overview
Advanced Topics in Mathematics covers a variety of upper-level mathematical concepts, making it a challenging yet rewarding class. The course typically explores topics such as linear algebra, multivariable calculus, and differential equations, pushing students to think critically about abstract mathematical ideas.
What You’ll Learn
This course goes beyond traditional high school math, introducing students to concepts that are typically encountered in college-level mathematics courses:
- Linear Algebra: Focuses on vector spaces, matrices, determinants, and eigenvalues.
- Multivariable Calculus: Expands on single-variable calculus by exploring functions of multiple variables, partial derivatives, and multiple integrals.
- Differential Equations: Deals with equations that describe how quantities change, often used in modeling real-world phenomena such as population growth or the motion of particles.
Challenges and Expectations
- Abstract Thinking: Advanced topics often involve abstract mathematical thinking and complex theories that require students to move beyond computation into proof-based learning.
- Proofs and Theorems: Many assignments will involve writing formal proofs, a skill that takes time and practice to develop.
- Real-World Applications: Students are often tasked with solving real-world problems, requiring them to apply mathematical concepts in practical scenarios, such as engineering or physics-based problems.
How to Succeed
Success in Advanced Topics in Mathematics relies heavily on critical thinking and the ability to understand abstract mathematical theories. It’s essential to develop a good understanding of the foundational concepts from previous math courses, as this course builds on those skills. Practice solving problems in a step-by-step manner, and don’t hesitate to seek help when you encounter difficult topics.
3. Honors Geometry
Overview
Geometry introduces students to the study of shapes, spatial relationships, and proofs. Honors Geometry, however, takes the subject to a more advanced level, requiring a deep understanding of formal proofs and logical reasoning. This class emphasizes spatial visualization, logical thinking, and the ability to construct and analyze geometric arguments.
What You’ll Learn
Honors Geometry typically covers:
- Euclidean Geometry: The study of plane figures such as triangles, quadrilaterals, and circles.
- Theorems and Proofs: A significant portion of the course is devoted to constructing and understanding formal geometric proofs.
- Coordinate Geometry: The study of geometric figures in the coordinate plane, combining algebraic concepts with geometric reasoning.
Challenges and Expectations
- Proofs and Logic: A major challenge in Honors Geometry is mastering the art of writing formal proofs. Students must develop the ability to logically explain and justify each step in solving geometric problems.
- Visual Thinking: Honors Geometry requires students to visualize shapes and spatial relationships, which can be difficult for those who are more comfortable with algebraic or numerical thinking.
- Rigorous Assignments: Homework assignments often involve complex problems that require creative thinking and persistence.
How to Succeed
To do well in Honors Geometry, practice is essential. Work on problems that involve different geometric figures, and focus on understanding the reasoning behind theorems rather than simply memorizing them. Collaboration with classmates and using visual aids, such as diagrams, can also help you grasp challenging concepts.
4. Statistics and Probability
Overview
Statistics and Probability is a course that deals with the analysis of data, uncertainty, and chance. This branch of mathematics is essential for students interested in fields such as economics, psychology, data science, and research. The course teaches students how to analyze data sets, draw conclusions from data, and make predictions based on probability.
What You’ll Learn
Statistics and Probability covers topics such as:
- Descriptive Statistics: Understanding measures of central tendency (mean, median, mode), variability (range, variance, standard deviation), and data distribution.
- Inferential Statistics: Making predictions and decisions based on sample data, including hypothesis testing and confidence intervals.
- Probability Theory: Exploring the mathematics of randomness, including probability distributions, expected values, and conditional probability.
Challenges and Expectations
- Data Interpretation: Students must be comfortable with analyzing large sets of data and understanding how to interpret results accurately.
- Critical Thinking: A key aspect of statistics is drawing meaningful conclusions from data, which requires strong critical thinking and problem-solving skills.
- Application-Based Learning: Unlike some other math courses, Statistics and Probability focuses on real-world applications, requiring students to relate theoretical concepts to everyday situations.
How to Succeed
Success in this course depends on a strong understanding of fundamental concepts and the ability to apply them to practical scenarios. Focus on learning how to interpret data and draw conclusions from it. Practice with real-world examples, and use tools such as graphing calculators and statistical software to aid in data analysis.
Conclusion
Math is a subject that can be both challenging and rewarding, especially when tackling some of the hardest courses in high school. Whether you're navigating the complex concepts of AP Calculus, exploring abstract theories in Advanced Topics in Mathematics, mastering logical proofs in Honors Geometry, or analyzing data in Statistics and Probability, these courses will push your problem-solving skills and expand your understanding of the mathematical world.
The key to succeeding in these challenging math classes is perseverance and a willingness to seek help when needed. Don't hesitate to reach out to your teachers, collaborate with classmates, or use online resources to enhance your understanding. Most importantly, approach these challenges with curiosity and determination, knowing that the skills you gain will serve you well in future academic pursuits.
Remember, the journey through advanced math classes may be tough, but the rewards—both personal and academic—are immense. Stay curious, stay determined, and keep pushing the boundaries of your mathematical knowledge. Your efforts will pay off in the long run!

.jpg)

.jpg)